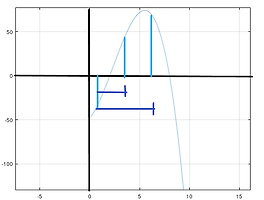
근 : f(x) = 0 이 되는 x
근을 구하는 방법
- 근의 공식 이용 : 2, 3, 4차 방정식
- 그래프적 방법: f(x) 그래프를 그려 x축과 만나는 점을 찾는다. (개략적, 정밀성 결여)
- 시행착오법: x의 값을 가정, f(x) = 0 이 되도록 반복하여 조정(실제 공학 응용에는 비효율)
- 수치 기법: 체계적 방법으로 근사적 근을 구함
구간법(bracketing method)
근을 포함하는 구간을 초기 가정값으로 시작하여, 체계적으로 구간의 폭을 줄여나간다.
연속된 함수는 구간의 약 끝점의 부호(sign)이 다르면 구간 내에 근이 있다.
함수의 근을 구하기 위해 그래프를 사용하는 방법
초기 가정 값을 제공한다.
함수의 특성과 수치기법들이 어떻게 해를 구하는지를 시각적으로 볼 수 있게 해준다.
그래프를 사용하는 방법
방정식 f(x) = 0 에 대한 근의 근사값을 찾기 위해 그래프를 그려 x축과 만나는 곳(f(x) = 0) 을 찾는다.
정밀하지는 않지만, 초기 가정값으로 사용 가능하다.
연속함수일 때,
- f(x-low) * f(x-up) > 0 (서로 부호가 같다) : 구간내에 근이 없거나 짝수개를 가진다.
- f(x-low) * f(x-up) < 0 (서로 부호가 다르다) : 구간내에 근이 홀수개 있다.

ex) f(x) = sin 10x + cos3x, 구간 [3,5] 에서 근을 구하라
MATLAB등을 이용하여 그래프를 그려 구한다.
x = 3:0.01:5;
y = sin(10*x) + cos(3*x);
plot(x,y)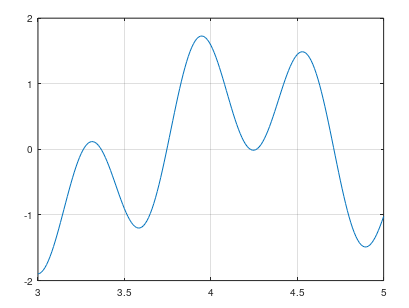

이분법(Bisection)
f(x)가 구간 [x-low, x-up]에서 실수이고 연속이며 f(x-low) * f(x-up) <0 일 때, 구간 내에 실근이 존재한다.
근을 구하기 위해 구간을 2개의 소 구간으로 나누고,부호가 바뀌는 소구간을 찾아 해당 구간을 다시 2분할하는 과정을 반복하여 근의 위치를 찾는다.
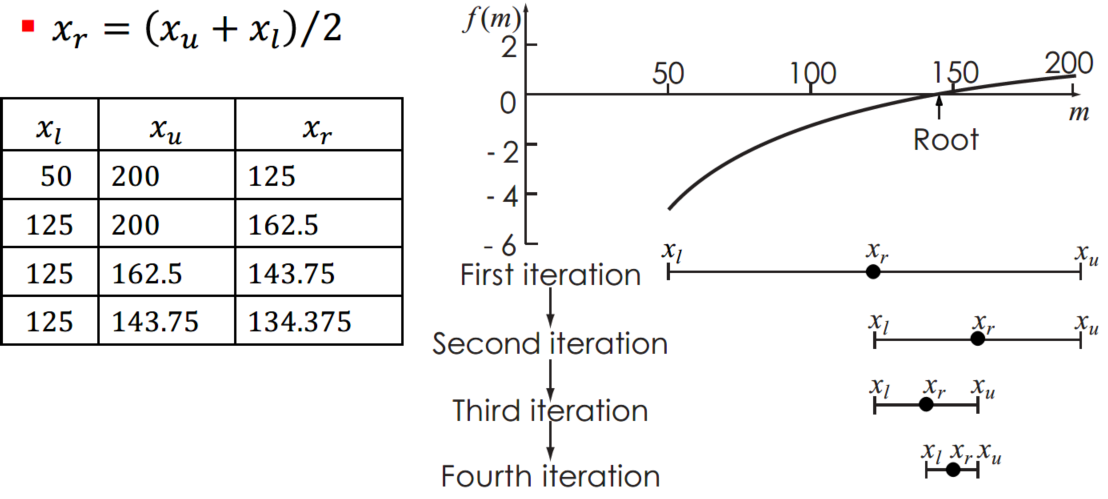
종료 판정 기준과 오차 추정
𝜀a(근사 백분율 상대오차) = | (x_new - x_old) / x_new | * 100%
𝜀a가 종료판정 기준 𝜀s 보다 작으면 반복을 종료한다.
이분법에서는 |𝜀t| <= |𝜀a| 가 보통 성립한다.
(오차를 구할 때 나누는 과정이 들어가는데, 참근이 0에 아주 가까운 값이면, 전체 값은 무한대로 발산 가능하므로 반드시는 아니다)

이분법 알고리즘
def Bisect( xl, xu, es, imax, f):
"""
@input xl 구간의 왼쪽
@input xu 구간의 오른쪽
@input es 종료 판정 기준
@input imax 최대 iteration 횟수
@input xr 초기값
@input f 계산에 사용되는 함수
@output xr 구간법을 이용해 얻은 해
@output fx xr에 의해 구한 f(xr)의 값
@output iter 답을 구할때 까지 반복 횟수
@inner ea 오차
@inner xrold 이전 해
"""
if f(xu) * f(xl) > 0:
print('no sign changed')
return
#맨 처음에 근 발견 못하면 종료
ea = 100
xr = xl
iter : int = 0
while True:
xrold = xr
xr = (xl + xu) / 2
iter += 1
if xr != 0:
ea = abs((xr - xrold) / xr) * 100 #상대오차
test = f(xl) * f(xr) # 양 끝값 곱해서 sign 정보 추출
if test < 0: # 부호 바뀜
xu = xr
elif test > 0: # 부호 안바뀜
xl = xr
else: # 해당 값 발견
ea = 0
if ea < es or iter >= imax:
break
fx = f(xr)
return (xr, fx, iter)ex)

fm = lambda m : sqrt(9.81 * m / 0.25) * tanh(sqrt(9.81 * 0.25/ m) * 4) - 36
print(Bisect(40,200,0.0001, 80, fm))
# 결과
# (142.73765563964844, -1.0997548471891605e-06, 21)
함수 계산의 최소화
함수의 계산을 최소화하는 수치 알고리즘이 필요하다.
실제 공학 문제를 풀기 위해서는 알고리즘을 수천, 수만번 수행해야 하며, 한번의 계산에도 상당한 시간을 요하는 코드로 구현되어 있는 경우가 있다.
위에서 언급한 이분법을 수정한 새로운 알고리즘은 xr에서 함수 값 fr 을 계산한 후 해당 값을 저장해 이후 계산에 사용하므로, 함수의 계산 횟수를 2n 에서 n + 1 정도, 즉 절반으로 줄이는 효과가 있다.
def Bisect2( xl, xu, es, imax, f):
if f(xu) * f(xl) > 0:
return 'no sign changed'
#맨 처음에 근 발견 못하면 종료
ea = 100
xr = xl
fl = f(xl) #새 코드
iter : int = 0
while True:
xrold = xr
xr = (xl + xu) / 2
fr = f(xr) #새 코드
iter += 1
if xr != 0:
ea = abs((xr - xrold) / xr) * 100 #상대오차
test = fl * fr # 양 끝값 곱해서 sign 정보 추출
if test < 0: # 부호 바뀜
xu = xr
elif test > 0: # 부호 안바뀜
xl = xr
fl = fr # 새 코드
else: # 해당 값 발견
ea = 0
if ea < es or iter >= imax:
break
fx = f(xr)
return (xr, fx, iter)가위치법 (False Position Method)
알고리즘은 xr의 계산법만 다르고 이분법과 같다.
|f(x)|가 0에 가까울 수록 근에 가깝다는 가정하에 닮은꼴 삼각형으로 직선의 교점을 추정한다.
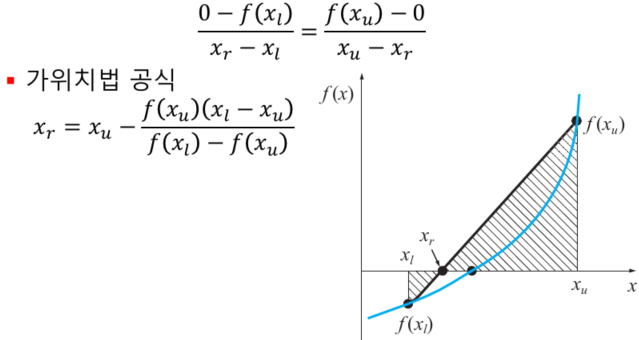
문제점
f(x_low) 이 f(x_up) 보다 0에 가깝다면 근이 xl에 가깝다는 전제를 벗어난다.
증분탐색법과 초기 가정값의 결정
증분 탐색은 선택한 범위의 한쪽 끝에서 출발해 매우 작은 양만큼 증가시켜가며 함수를 계산한다. 함수의 부호가 바뀌면 근은 증분 내에 있다고 가정한다. 이때 증분 탐색의 시작과 끝의 x 값을 x_low, x_up 즉 구간 방법의 초기 가정값으로 사용한다.
증분량이 너무 작으면 계산 시간이 오래 걸리고, 너무 크면 근을 놓칠 수 있으므로 적당한 증분량을 결정해야 한다.
(단, 중근의 경우 증분구간의 크기와 관계없이 놓치기 쉽다.)
'수학 > 수치해석' 카테고리의 다른 글
| [수치해석 06] 행렬식에서 근 구하기 (0) | 2021.09.30 |
|---|---|
| [수치해석 05] 선형 대수 방정식 (0) | 2021.09.30 |
| [수치해석 04] 개구간법(Open Methods) (0) | 2021.09.27 |
| [수치해석 02] 절단오차와 Taylor 급수 (0) | 2021.09.23 |
| [수치해석 01] 근사값과 반올림 오차 (0) | 2021.09.16 |