Crammer 공식
연립 선형대수 방정식에서 각각의 미지수는 행렬식의 비로 표시될 수 있다.

행렬이 위와같이 주어질 때,

이고,

미지수 소거법
전진 소거, 후진 대입


(원래) Gauss 소거법
- 미지수의 전진소거, 상삼각행렬 형태로 변형
- 후진 대입 : 올라가면서 변수를 대입하여 값을 구한다.

피벗 . pivot
특정 계산을 수행하기 위한 알고리즘에 의해 먼저 선택된 행렬의 요소
피벗 원소 : 소거시키는 기준이 되는 원소
피벗 방정식 : 피벗 원소가 있는 방정식
피벗 행 : 피벗 원소가 속한 행
정규화(normalization) : 피벗 행의 원소를 피벗 원소로 나누는 과정. 피벗 원소의 계수가 1이 된다.


후진 대입 (back substitution)

아래에서 구한 원소를 통해 위의 원소를 구한다.
(원래) Gauss 소거 알고리즘
전진소거, 후진 대입의 과정을 고려

알고리즘 파이썬 구현 코드
def Gauss(arr: list[list], ans: list):
'''
@input arr: list[list]
반드시 정사각행렬
arr의 행 = 열
len(arr의 열) = len(ans의 열)
@input ans : list
방정식의 해를 1열의 배열로 나타낸 것
@output
방정식의 근
'''
if len(arr) != len(ans):
return
n = len(ans)
# 전진소거 과정
for k in range(n-1): # 배열은 0 ~ n-1 인덱스를 가진다...
# 하나의 열 단위로 소거하는 과정.
# 만약 a11만 남기려면, a21...은 소거해야 한다.
for i in range(k+1, n): # 각 행의 원소를 소거하는 과정
factor = arr[i][k]/arr[k][k]
# 원소를 남기고 싶은 행에 factor을 곱해 각 행에서 빼줄 것이다.
for j in range(k+1, n):
# 각 행의 원소들로부터 pivot 행의 원소들에 factor을 곱한 값을 뺀다.
arr[i][j] -= factor * arr[k][j]
ans[i] -= factor * ans[k]
# 후진 대입 과정
result = [0 for x in range(n)] # 방정식의 근을 위한 공간 생성
result[n-1] = ans[n-1] / arr[n-1][n-1]
for i in range(n-1, -1, -1): # 뒤의 값부터 계산 수행
sum_ = ans[i]
for j in range(i+1, n):
sum_ -= arr[i][j] * result[j]
result[i] = sum_ / arr[i][i]
return result

arr = [
[3, -0.1, -0.2],
[0.1, 7, -0.3],
[0.3, -0.2, 10]
]
ans = [7.85, -19.3, 71.4]
result = Gauss(arr,ans)
print(result)
# 출력 결과 [3.0, -2.5, 7.000000000000002]
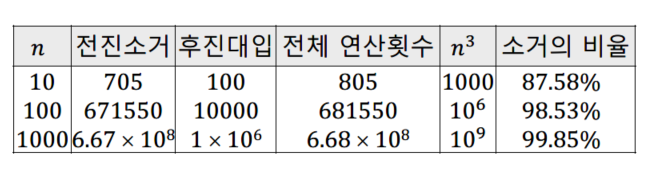
알고리즘 시간 복잡도
특정 알고리즘에 대해 시간 복잡도는 최고차항(값의 변화에 가장 영향을 많이 주는 항)의 영향을 받으며, 나머지 요소는 입력의 규모가 커짐에 따라 사소해지므로, 무시한다.
ex)

위 (원래) 가우스 소거법의 식에서 발생하는 시간 복잡도는 다음과 같다.

시스템(연립 방정식)이 커질 수록 연산시간이 크게 증가한다.
대부분의 연산은 전진 소거 단계에서 발생한다.
소거법의 문제점
원래의 가우스 소거법을 통해 많은 연립방정식의 해를 구할 수 있으나, 컴퓨터 프로그램으로 구현하는 단계에서 발생할 수 있는 문제점이 존재한다. 해당 문제점은 다음과 같다.
1. 0으로 나누는 경우 -> 피벗화로 해결

첫번째 열을 정규화 할때, x1 자리의 계수가 0이므로, 위의 알고리즘을 따르면 0으로 나누는 일이 발생.
계수가 0에 가까운 경우에도 비슷한 문제가 발생한다
이 경우, 피벗화를 사용한다.
2. 반올림 오차 -> 피벗화로 완화
계산 결과를 판단할 때 반올림 오차를 고려해야 한다.
많은 수의 연립방정식을 푸는 과정에서 각 결과는 이전 결과에 의존하므로, 초기 단계의 오차가 전파될 수 있다.
해를 원래 연립방정식에 대입하여 무시할 수 없는 크기의 오차가 발생하는지 점검해봐야 한다.
3. 불량조건 시스템 -> 축척으로 추정
계수의 작은 변화가 해에 커다란 변화를 일으키는 경우
반올림 오차에 의해 발생한 계수의 작은 변화가 커다란 해의 오차를 가져올 수 있다.

우량조건 시스템(well-conditioned system) : 계수 값의 변화에 따라 약간의 변화만 발생.
불량조건 시스템의 행렬식
직선의 기울기가 거의 같으면 두 선의 교차점을 알기 매우 어렵다.
행렬식은 0에 가까워진다.

행렬식에 대한 축척화(scaling)
행렬식은 계수의 크기에 영향을 받는 상대적인 값이다.
예를 들어 2차 연립방정식에서 각 계수에 10을 곱하면, 행렬식은 100배 증가하게 된다.
따라서, 행렬식이 0에 가까운지 여부만으로는 연립방정식이 시스템에 속하는지 알 수 없다.
이를 위해 행렬식을 표준화 할 필요가 있다.
각 방정식의 계수의 최대값을 1이 되도록 축적화 한 후 행렬식을 구하여 불량 조건을 판단한다.



Gauss 소거법을 이용한 행렬식의 계산
삼각행렬의 행렬식은 대각 원소의 곱으로 계산

Gauss 소거법의 전진소거 단계만으로는 부호가 바뀌지 않는다.
부분 피벗팅을 사용한 경우, 행렬식의 부호는 행이 바뀐 수에 따라 변한다.

특이 시스템(singular system)
특이 시스템의 행렬식은 0
삼각행렬의 행렬식은 대각선 요소의 곱
소거 단계에서 대각선 요소에 0이 생긴다면, 특이 시스템이다.(피벗팅은 기본 가정한다)
해를 개선하는 기법
- 더 많은 유효숫자 사용 : 정밀도 증가를 통해 불량조건의 가능성을 완화 but 계산/메모리 증가
- 피벗화 : 방정식의 순서를 바꾸는 방법
- 축척화 : 표준화(최대 계수 = 1로 변경)
피벗화
기존 Gauss 소거법에서는 주대각선에 0 성분이나 0에 가까운 성분이 존재하면 문제가 발생했다.
이런 문제를 해결하기 위해 피벗화를 사용한다.
부분 피벗화
피벗 요소의 밑 열에서 절대값이 가장 큰 계수를 찾은 후 가장 큰 요소가 피벗 요소가 되도록 행의 위치를 교환하는것.
완전 피벗화
행 뿐만 아니라 열에서도 가장 큰 요소를 찾아 위치를 교환하는 것. 프로그램이 복잡해져, 잘 사용하지 않는다.
행 -> 방정식의 순서, 열 -> 변수의 순서.
ex)
피벗팅 이전




피벗팅 이전의 값은 유효숫자수에 민감한 결과가 나왔다.
피벗팅 이후




피벗팅 이후의 값은 유효숫자에 덜 민감했다.
의사 코드

순회를 통해 가장 큰 피벗을 찾은 후, 자기 자신이면 바꾸지 않고, 아니면 피벗과 해당 행 전체를 바꾼다.
축척화
각 방정식의 계수의 최대값이 1이 되도록 축척화하는 것.
행렬식의 크기를 표준화하는데 유용하게 사용된다.
시스템 내의 몇 개의 방정식들이 유난히 큰 계수를 가지면 피벗화 및 반올림 오차에 큰 영향을 미친다.
이 경우, 계수는 축척화하여 피벗화의 기준으로 사용하되, 실제 소거 및 대입에는 원래 계수를 사용한다.



Gauss 소거법 알고리즘
축척화 한 계수를 기준으로 원래 방정식을 피벗화(c) 한다.
대각선 항에 0에 가까운 값(불량 조건) 이 있는지 체크한다.




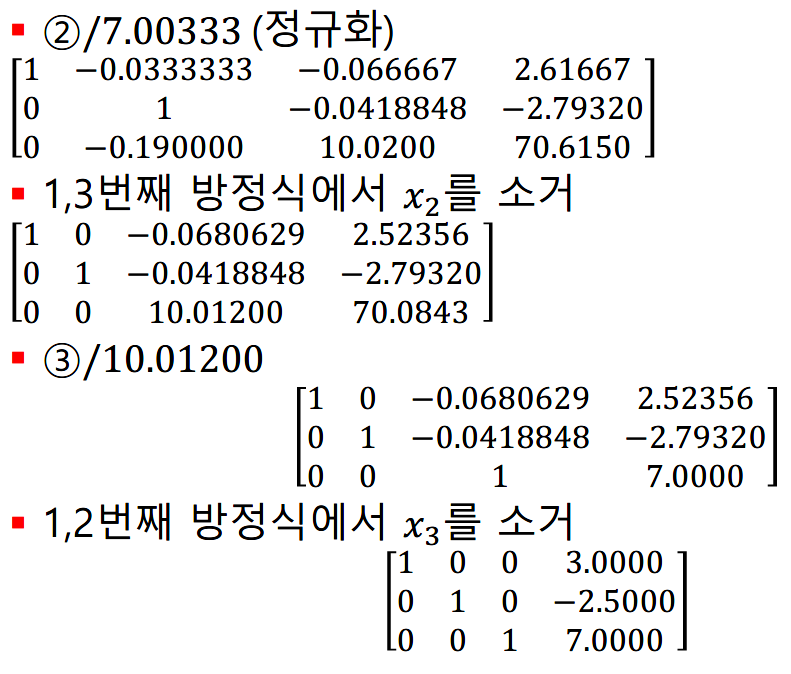
Gauss-Jordan 소거법
각 행에 대해 다음을 반복하여 단위 행렬을 얻는다.
- 피벗 행을 피벗 요소로 나누어 정규화한다.
- 피벗 행을 제외한 모든 방정식으로부터 미지수를 소거한다.


'수학 > 수치해석' 카테고리의 다른 글
| [수치해석 08] 특수 행렬과 Gauss-Seidel법 (0) | 2021.10.26 |
|---|---|
| [수치해석 07] LU분해법과 역행렬 (0) | 2021.10.12 |
| [수치해석 05] 선형 대수 방정식 (0) | 2021.09.30 |
| [수치해석 04] 개구간법(Open Methods) (0) | 2021.09.27 |
| [수치해석 03] 방정식의 근 (0) | 2021.09.23 |