수치적으로 적분하게 되는 데이터는 테이블 형태와 함수 형태로 나뉜다. 테이블 형태는 정해진 이산 개수의 데이터에 기반하여 적분하게 되고, 함수는 함수 식에 기반하여 생성된 점을 이용하여 적분하게 된다.
수식에 대한 Newton-Cotes 알고리즘

합성 사다리꼴 공식 및 Simpson 공식은 함수에 대해서도 적용할 수 있으나, 구간이 크게 증가함에 따라 반올림 오차가 역으로 증가하여 오차가 더 높아지는 현상이 발생한다. 따라서, 높은 효율성 및 작은 오차가 필요한 경우 부적합하다.
파이썬 알고리즘
from typing import Callable
def TrapEq(f : Callable[[float], float], n: int, a:float, b:float):
'''
@params f : 사용되는 함수
@params n : 구간의 개수
@params a : 구간의 시작
@params b : 구간의 끝
@return : Newton-Cotes 법을 함수에 대해 적용한 결과
'''
h = (b - a)/n # 구간 간격 생성
x = a #시작점
sum = f(x) # f(a) 지정
for i in range(1,n): # 1 ~ n-1
x = x + h #구간 증가
sum = sum + 2 * f(x) # 중간 구간 더하기
sum = sum + f(b) # 마지막 값 더하기
result = h* sum / 2
return result
if __name__ == "__main__":
fn : Callable[[float],float] = lambda x : 0.2 + 25*x - 200*pow(x,2) + 675*pow(x,3) - 900*pow(x,4) + 400 *pow(x,5)
fn2 : Callable[[float, float], float] = lambda x0, x1 : 4/3 * x0 - 1/3 * x1
fn3 : Callable[[float, float], float] = lambda x0, x1 : 16/15 * x0 - 1/15 * x1
f0 = TrapEq(fn,1,0,0.8)
f1 = TrapEq(fn,2,0,0.8)
f2 = TrapEq(fn,4,0,0.8)
f10 = fn2(f1,f0)
f11 = fn2(f2,f1)
f20 = fn3(f11,f10)
print(f"{f0:.4f}")
print(f"{f1:.4f}")
print(f"{f2:.4f}")
print(f"{f10:.4f}")
print(f"{f11:.4f}")
print(f"{f20:.4f}")x^2 + 2x + 1 에 대해 계산...
결과

Romberg 적분법
함수의 수치적분을 효율적으로 구하는 방법으로, 사다리꼴 적분 공식을 연속적으로 적용하는 방법이다. 수학적 조합을 통해 계산량이 감소, 결과는 좋다. 개인적으로 Newton 보간 다항식과 비슷하게, 이전 항을 기반으로 새로운 항을 계속 만들어 나간다.
Richardson 보외법(Extrapolation)
두개의 적분 값을 이용하여 정확한 근사값을 계산하는 방법으로, 각 적분 값은 합성 사다리꼴 공식을 이용해 구한다.
합성 사다리꼴 적분 공식에 대해 실제값 : I , 추정값 : I(h) , 오차 : E(h) 라 하면,

구간의 갯수 n을 다르게 하더라도 실제 값은 바뀌지 않으므로,

이때 합성 사다리꼴의 오차는 다음과 같이 알려져 있다.

f'' 이 간격의 크기 h 와 관계 없는 상수라고 가정하고 h에 대해 식을 수정하면 다음과 같은 식들이 성립한다.

따라서 위에서 얻은 결과를 바탕으로 식을 정리하면,

해당 식은 O(h4) 의 정확도를 보이는 것으로 알려져 있다.
ex)

고차 확장
2개의 * O(h4) -> O(h6)

2개의 O(h6) -> O(h8)

ex)

Romberg 적분 알고리즘
우수한 적분값(간격의 수가 더 많은 적분)에 보다 큰 가중치를 주어, Richardson 보외법을 일반화한 표현법.

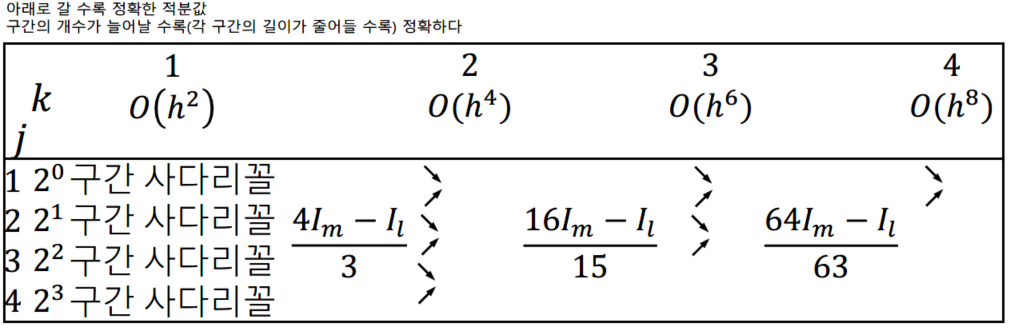
ex)

Romberg 적분의 종료 판정 기준

새로운 추정값을 구한 뒤, 이전 추정값 중 최선인 값과 비교한다.
예를 들어 위의 2번 반복 기준에서 1.640533은 새로운 추정값이고, 이전 추정값 중 최선의 값은 1.623467이다.
따라서 이 값들을 기반으로 계산하면,

파이썬 알고리즘
from typing import Callable
from Newton_Cotes_func import TrapEq
def Romberg_Int(f: Callable[[float], float], a: float, b: float, maxit: int, es: float):
'''
@params f : 사용되는 함수
@params a : 구간의 시작
@params b : 구간의 끝
@param maxit : 최대 반복 회수
@param es : 반복 조건
@return : Romberg 적분 법을 함수에 대해 적용한 결과
'''
fval : list[list[float]] = []
# 각 함수 값이 저장되는 장소
# 2차원 배열 형태로 설계된다.
n = 1 # 구간의 개수
fval.append([])
fval[0].append(TrapEq(f, n, a, b)) # I 0,0
iter = 0 # 현재 반복 회수
while True:
fval.append([]) # 새로운 차수가 생긴다.
iter = iter + 1
n = 2**iter
# 첫번째 배열에 초기 값이 들어간다.
fval[0].append(TrapEq(f, n, a, b))
for k in range(1, iter + 1):
j = iter - k
fval[k].append((4**(k)*fval[k-1][j+1] - fval[k-1][j])/(4**(k) - 1)) # 다음 차수 계산
ea = abs((fval[iter][0] - fval[iter-1][1])/fval[iter][0]) * 100 #오차 계산
# 현재 배열 및 오차 출력
print(f'iter[{iter:3d}] : ea = {ea}')
print("arr")
for elem in fval:
for val in elem:
print(f"{val:.4f}", end ='\t')
print()
print('\n\n')
if iter >= maxit or ea <= es : #종료조건 판단
break
return (iter, fval[iter][0])
if __name__ == '__main__':
fn : Callable[[float],float] = lambda x : 0.2 + 25*x - 200*pow(x,2) + 675*pow(x,3) - 900*pow(x,4) + 400 *pow(x,5)
a = 0
b = 0.8
print(Romberg_Int(fn,a,b,100,1))결과

Gauss 구적법


사다리꼴 공식의 경우 기본 점이 끝 점으로 고정되어 있기 때문에 종종 큰 오차를 초래한다. 따라서 두 점을 양 끝점으로 고정하는 대신 곡선상의 임의의 두 점을 선택하여 양의 오차와 음의 오차가 균형을 이루도록 위치를 조정하게 된다.
이러한 전략을 구현하는 방법을 통칭하는 것이 Gauss quadrature, 가우스 구적법이다.
미정계수법 ( method of undetermined coefficents )
적분할 함수에 대해 정확한 결과를 산출하기 위해 상수 c 를 결정하는 방법. 상수의 갯수만큼 방정식이 필요하다.

Gauss-Legendre 공식을 이용한 구적법
Gauss-Legendre 공식 Legendre 공식의 구간을 [-1, 1] 로 정규화하여 적분하는 공식으로, 점의 개수에 따른 계수 및 대입할 값이 이미 알려져 있다. (아래 표 참조)
이 공식은 선형으로 나타나는 방정식(y = w0x0 + w1x1 + w2x2 + ... )의 계수를 결정하기 위한 방정식이다.


2점 Guass-Legendre 공식의 유도
c0, c1, x0, x1 가 고정되지 않았으므로, 아래 4개의 식을 연립한다.

이를 연립하면, 다음과 같은 결과가 나온다.

이러한 식의 연립을 이용하여 2점 이상의 항에 대해서도 미지수 및 계수를 위의 표처럼 구할 수 있다.
일반 적분 구간의 선형 변환

해당 공식은 [-1, 1] 범위에서 작동하지만, 우리의 적분 식은 [a, b] 에 대해 나타나므로, 이를 정규화해야 한다.
이때 [a, b] 에서 정의되는 변수 x을 [-1, 1] 에서의 변수 xd 에 대해 나타내고, 식을 푼다.

위에서 얻게 된 x 및 dx을 원래 식에 대입하여 사용한다.
ex)

Gauss 구적법은 적분구간 내에서 부등간격으로 분포된 점들에 대한 계산이 필요하다. 표에 지정된 값들을 다 구해야 하기 때문이다. 따라서, 함수 식이 알려지지 않은 경우에는 사용할 수 없다.
'수학 > 수치해석' 카테고리의 다른 글
| [수치해석 17] Runge kutta법 (0) | 2021.11.30 |
|---|---|
| [수치해석 16] 수치미분 (0) | 2021.11.25 |
| [수치해석 14] Newton-Cotes 적분 공식 (0) | 2021.11.18 |
| [수치해석 13] 스플라인 보간법 (0) | 2021.11.16 |
| [수치해석 12] 보간법 (0) | 2021.11.09 |




