특정 행렬들은 특수한 구조를 가지고 있는데, 이런 행렬들을 특수 행렬이라고 부른다.
띠행렬
주 대각선을 중심으로 한 띠(band)를 제외한 모든 요소가 0인 정사각형 행렬.
주 대각선의 원소 중 일부가 0인지 여부와는 관계 없이, 띠를 제외한 요소가 0이면 된다.
피벗화(행끼리 위치를 바꾸는 것)가 필요하지 않다면, 0인 요소에 대해서는 연산을 수행하지 않는 알고리즘이 가능.
대역폭(bandwidth, BW)과 반대역폭(half-bandwidth, HBW)는 다음과 같은 관계를 만족한다.
BW = 2HBW + 1

삼중대각 시스템
띠의 폭이 3인 띠행렬로, Thomas 알고리즘에 의해 해를 구할 수 있다.

Thomas 알고리즘
삼중대각 시스템의 해를 구하는 알고리즘으로, O(n)의 시간 복잡도를 지닌다. (보통 O(n3)의 복잡도)
공식 자체는 LU분해법을 통해 해를 구하는 것과 크게 다르지 않으나, 각각의 원소의 값을 구하는 것이 간단하다.
공식으로부터 값이 도출되는 단계는 가우스 소거를 한다고 생각하고 소거해보면 아주 당연하다.
기존 LU 분해에서 L의 성분들은 factor에 해당하고 U의 성분들은 가우스 소거에 의한 결과가 저장되는데, 이러한 원리에 삼중대각 시스템이라는 특수한 상태가 맞물려 공식화가 가능한 것 뿐이기 때문이다.
분해 영역
ek = ek / fk-1
fk = fk - ek * gk-1
전진 대입 영역
rk = rk - ek*rk-1
후진 대입 영역
xn = rn/fn
xk = (rk - gk * xk+1) / fk
알고리즘



예시





대칭 행렬
[A] = [A]T 인 행렬로, 주대각선에 대해 성분들의 값이 일치한다.
특정 조건(구체적으로는 positive definitive)을 만족하면 이런 행렬은 [L][L]T 꼴로 분해할 수 있는데,
[L] 하나에 대해서만 계산하면 되기 때문에 계산 시간 및 저장 공간이 기존 방식에 비해 절반으로 감소한다.
Cholesky 분해법
위에서 언급한 분해 방식이다. positive definitive 조건을 만족하는 대칭행렬에 대해, 각각의 항은 다음과 같다.


기본적으로, 위 공식 역시 양변을 정리하면 도출된다.
1. aki의 도출 과정


왜 i 까지일까? 기본적으로 이 알고리즘은 하삼각행렬 L을 만드는 알고리즘이다. 따라서 모든 경우에 대해 i <= k 이다.
이때 ( i, i ) 는 주대각성분이 위치하는 인덱스인데, 기본적으로 L 행렬은 주대각성분 위쪽의 성분이 모두 0이므로, 해당 인덱스 이상의 값에 대해서는 계산 결과가 모두 0이 나올 것이므로, 계산할 필요가 없다. 따라서 마지막 인덱스는 i이다.
2. akk의 도출 과정
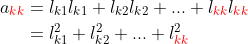


동일한 원소를 가진 행에 대해 계산하므로, 각각은 제곱 형태로 곱해진 모습을 가진다.
우리가 구하고자 하는 곱 역시 제곱에 대해 나타나므로, 해당 값에 대한 제곱근 형태로 나타낸다.
(알고리즘)

예시







Gauss-Seidel법
[A]{x} = {B}의 해를 구하기 위한 반복법으로, 초기 근을 가정한 후에 더 좋은 근을 계속 추정해나가는 방식이다.
각 근들에 대해, 현재 근사해를 구할 때 현재 구한 값을 사용한다는 점에 주목하자.


이때, 각각의 근들에 대해 전부 아래 조건을 만족할 때, 반복을 종료한다.

Jacobi 반복법
기본적으로 Gauss-Seidel 법과 큰 차이가 없으나, 근을 구할 때 항상 이전 근사해를 사용한다.

Gauss-Seidel 법의 수렴 여부 판정
대각 지배 시스템(Diagonally dominant system)
각 방정식의 대각 계수의 절대값이 해당 방정식의 다른 계수의 절대값 합보다 큰 시스템.
Gauss-Seidel 법에 대하여, 각 방정식이 대각 지배 시스템이면 방정식은 수렴한다.

이완법을 사용한 수렴성 개선
새로운 x의 값을 계산한 후, 그 값을 현재와 직전 계산된 결과의 가중 평균으로 두는 방식.

가중인자 λ: 0 < λ <2
- λ = 1 : Guass-Seidel 법과 동일하다.
- 0 < λ < 1 : 하이완법(underrelaxation). 수렴하지 않는 시스템을 수렴하거나, 진동 속도를 감쇠-수렴 빠르게
- 1 < λ < 2 : 상이완법(overrelaxation). 바른 해를 향하지만 속도가 느릴 때, 수렴 속도를 증가시키기 위해
알고리즘
! 대각 지배 시스템이 아니라면, 수렴을 보장할 수 없다.

대각선 요소로 미리 나눈다 ( dummy, 1~7 )
초기 xold에 해당하는 값을 생성 ( sum, 8~14 )

반복 시작 ( iter = 1 )
보초 값 sentinel 지정, 끝날 때까지 1이면 반복 중지.
'수학 > 수치해석' 카테고리의 다른 글
| [수치해석 10] 최소 제곱 회귀 분석 (0) | 2021.11.04 |
|---|---|
| [수치해석 09] 비구속 최적화 (0) | 2021.10.28 |
| [수치해석 07] LU분해법과 역행렬 (0) | 2021.10.12 |
| [수치해석 06] 행렬식에서 근 구하기 (0) | 2021.09.30 |
| [수치해석 05] 선형 대수 방정식 (0) | 2021.09.30 |



