https://www.acmicpc.net/problem/2292
- 입력: N(1 ≤ N ≤ 1,000,000,000)
- 출력: 주어진 방까지 이동할 때 최소 방의 수

최소로 이동하는 방의 수는 다음과 같은 규칙을 가지고 있다.
| 방 번호(N) | 이동하는 수(K) |
| 1 | 1 |
| 2 ~ 7 | 2 |
| 8 ~ 19 | 3 |
| 20 ~ 37 | 4 |
위 숫자에는 어느 정도 규칙성이 있다. 범위 내 마지막 번호(E) - 1 => 6의 배수이다.
| 방 번호(S ~ E) | (E - 1) / 6 | 이동하는 수(K) |
| 1 | (1 - 1) / 6 = 0 | 1 |
| 2 ~ 7 | (7 - 1) / 6 = 1 | 2 |
| 8 ~ 19 | (19 - 1) / 6 = 3 | 3 |
| 20 ~ 37 | (37 - 1) / 6 = 6 | 4 |
(E - 1) / 6 값은 1 ~ 이동하는 수 K에 대해 1 ~ (K - 1) 까지의 등차수열 = (k - 1) * k / 2에 해당한다.
| 방 번호(S ~ E) | (E - 1) / 6 | (K-1) * K / 2 | 이동하는 수(K) |
| 1 | (1 - 1) / 6 = 0 | (1 - 1) * 1 / 2 = 0 | 1 |
| 2 ~ 7 | (7 - 1) / 6 = 1 | (2 - 1)(2) / 2 = 1 | 2 |
| 8 ~ 19 | (19 - 1) / 6 = 3 | (3 - 1) * 3 / 2 = 3 | 3 |
| 20 ~ 37 | (37 - 1) / 6 = 6 | (4 - 1) * 4 / 2 = 6 | 4 |
X = (E - 1) / 6 이라 두고 K에 대해 식을 정리하면, K^2 - K - 2X = 0이 된다. 이때 2차방정식 근의 공식은 다음과 같다.

이 식에 대해 a = 1, b = -1, c = -2X를 대입하고, 양의 근을 선택하자.

식이 깔끔하게 정리되었다. X = (E - 1) / 6 을 구해서 넣으면 K 값을 바로 얻을 수 있다. 그런데, 각 상황에 맞게 E를 얻는 것은 쉽지 않다.
사실 E를 직접 얻을 필요는 없다. 범위(S ~ E) 내 값을 연산하면 이전 범위보다 큰 값을 가지며, N = E일 때 K가 정수 값을 가지므로 올림(ceil) 보정을 통해 K를 얻을 수 있게 된다.
from math import ceil, sqrt
def getPositiveRoot(x: float) -> float:
return (sqrt(1 + 8*x) + 1) / 2
for i in range(1, 21):
result = getPositiveRoot((i - 1) / 6)
print(f"{i}, {result:.3f}, {ceil(result)}")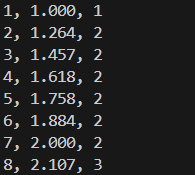


현재 문제를 푼 코드는 다음과 같다.
from math import sqrt, ceil
N = int(input())
def getPositiveRoot(x: int) -> float:
return (sqrt(1 + 8*x) + 1) / 2
# 1은 기본 값
result = ceil(getPositiveRoot((N - 1) / 6))
print(result)
아이디어 요약
- 방 번호와 이동 거리 사이에서 (E - 1)이 6의 배수라는 규칙을 파악
- (E - 1) / 6 = X 로 둘 때 X = (K - 1) * K / 2 (등차수열) 관계에 있음을 파악
- 2차방정식 근의 공식을 통해 K에 대해 식을 정리
- 올림(Ceil)을 통해 이동 거리 K 획득하는 일반식 획득
'CS > 알고리즘&문제풀이' 카테고리의 다른 글
| [프로그래머스 SQL] 오랜 기간 보호한 동물(2) / TIMESTAMPDIFF / TO_SECONDS (1) | 2024.05.13 |
|---|---|
| [프로그래머스] 숫자 변환하기 (0) | 2023.07.28 |
| [프로그래머스] 방문 길이 (0) | 2023.07.23 |
| [백준] 4948, 베르트랑 공준 (0) | 2023.07.04 |
| [프로그래머스] 마법의 엘리베이터 (1) | 2023.05.11 |

