https://school.programmers.co.kr/learn/courses/30/lessons/169198
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
원쿠션으로 주어진 공을 맞출 때, 공이 이동하는 최소값을 찾는 문제이다. 문제 설명 중 입사각 및 반사각이 동일하다는 정보가 있는데, 이 정보를 가지고 각도를 어떻게 구해보겠다고 하면 문제가 산으로 가기 쉽다.
우선 문제를 생각하기 전에, 입사각과 반사각에 대해 다시 떠올려보자.
https://terms.naver.com/entry.naver?docId=2039087&cid=47308&categoryId=47308
입사각과 반사각
알렉산드리아로 유학 온 그리스의 수학자 헤론은 빛이 반사될 때 입사각과 반사각이 같음을 알아냈습니다. 빛이 거울에 반사될 때 입사각과 반사각이 같은 이유는 무엇일까요? 이에 대해 헤론
terms.naver.com

언젠가 과학 시간에 입사각 반사각 수업을 들었던 것 같은데, 입사각 및 반사각은 동일하며, 빛이 반사되지 않고 직진했다고 가정할 경우 두 적색 직선은 대칭하는 위치에 있다. 위 문제에서는 이 성질을 이용할 예정이다.
두 공의 X 또는 Y 좌표가 동일하지 않은 경우

먼저 두 공의 x 및 y 좌표가 다른 경우를 생각해보자. 이 경우 두개의 공 중에서 하얀 공을 원래 위치에서 축에 대해 대칭이동한 후, 두 공 사이에 직선을 그리면 해당 직선은 입사각과 반사각을 고려할 때와 동일한 길이를 가진다.
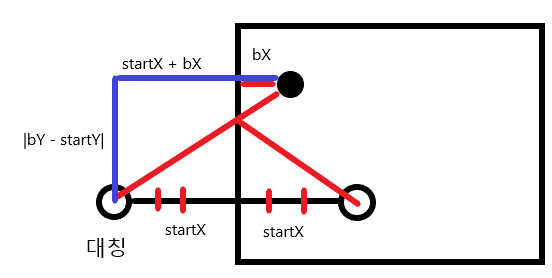
이때 흰 공의 좌표를 (startX, startY), 검은 공의 좌표를 (bX, bY)로 두면, 대칭된 흰공과 검은 공 사이의 x방향 길이는 startX + bX, y방향 길이는 |bY - startY|가 된다. 이 경우 길이 제곱은 (startX + bX)^2 + (bY - startY)^2 가 된다.

그런데 흰 공을 반대로 대칭시키는 거리가 더 가까울 수도 있으므로, 반대 방향에 대해서도 구해보자. 이 경우 오른쪽 선은 흰 공과 m - startX, 검은 공과 m - bX 만큼의 거리가 떨어져 있다.
위와 동일하게 계산하면 길이의 제곱은 (2m - startX - bX)^2 + (bY - startY)^2가 된다. 이때 2m - startX - bX <= startX + bX, 즉 startX + bx >= m이면 왼쪽이 더 짧으므로 위 식을 선택하고, 아니면 아래 식을 선택하여 x축 방향에 대한 최소 거리를 얻을 수 있다.이 과정은 y축에 대해서도 동일하게 적용된다.
두 공의 X 또는 Y 좌표가 동일한 경우
두 공의 X 또는 Y 좌표가 동일한 경우, 거리가 가깝다고 짧은 거리를 선택할 수 없다. 흰 공이 벽에 닿기 전에 검은 공과 부딪칠 수 있기 때문이다.

이 경우에는 두 공의 x 좌표 dX와 startX 좌표를 비교하여 startX > dX라면 흰 공이 오른쪽에 부딪쳐야 하므로 (2m - startX - dX)^2, 반대의 경우 왼쪽에 부딪치므로 (dX + startX)^2가 된다. y축 방향에 대해서도 동일하게 적용된다.
모서리에 부딪칠 수 있는 경우
| #추가: 모서리에 부딪치는 경우 가로, 세로로 대칭하는 경우보다 길이가 길기 때문에 고려하지 않아도 된다고 한다. 가로 또는 세로 방향의 경우 가로와 세로 중 한 방향으로만 대칭되지만, 대각선은 가로 + 세로 모두 대칭되므로 이동 거리가 필연적으로 길어진다. 따라서 이 문제에서 대각선의 경우 구하지 않아도 정상적으로 동작한다고 한다. |
두 공이 각 모서리에 대해 일직선상에 있는 경우, 모서리로도 흰 공을 쏠 수 있다. 흰 공과 모서리, 검은 공과 모서리의 기울기를 구했을 때 동일하면 일직선상에 있다고 판단할 수 있으므로, 이런 경우에는 모서리로 공을 쏘는 상황도 고려한다. 나는 각 모서리 좌표를 따로 배열에 저장해서 각 공마다 해당되는 상황이 있는지 검사했다.


이때 모서리를 선택하기 위한 조건은 하나 더 있다. 반드시 흰 공이 검은 공보다 모서리에 가까이 있어야 한다. 만약 흰공이 더 멀리 있다면 모서리로 흰 공을 날릴 때 반드시 검은 공에 맞게 되므로 원쿠션에 해당하지 않기 때문이다.
모서리와 검은공의 좌표 차이 bdx와 모서리와 흰공 사이의 x 좌표 차이 cdx을 비교하여 cdx < bdx인 경우, 즉 흰 공이 더 가까운 경우 검사 조건에 포함한다.
코드
내가 작성한 작성한 코드는 다음과 같다.
def solution(m: int,n: int,startX: int,startY: int,balls: list[list[int]]):
result = []
corner = [[0,0], [m,0], [0,n], [m,n]]
for bx, by in balls:
minlist = []
# x축 방향. 2m - b - s 와 b + s를 비교한다.
xmin = (by - startY)**2 + ((bx + startX)
if (by != startY and (bx + startX) <= m)
# y 다르고 왼쪽 길이가 더 짧은 경우
or (by == startY and startX < bx)
# y 같고 흰 공이 더 왼쪽에 있는 경우
else (2*m - bx - startX))**2
minlist.append(xmin)
# Y축 방향.
ymin = (bx - startX)**2 + ((by + startY)
if (bx != startX and (by + startY) <= n)
or (bx == startX and startY < by)
else (2*n - by - startY))**2
minlist.append(ymin)
# 모서리를 고려하는 경우
for cx, cy in corner:
scx, scy = startX - cx, startY - cy
bcx, bcy = bx - cx, by - cy
# 기울기 같고 유저 공이 모서리에 더 가까운 경우
if scy / scx == bcy / bcx and abs(scx) < abs(bcx):
cur = (scy + bcy)**2 + (scx + bcx)**2
minlist.append(cur)
result.append(min(minlist))
return result더 좋은 코드가 있을 것 같으나, 이 정도면 직관적인 수준인 것 같다.
'CS > 알고리즘&문제풀이' 카테고리의 다른 글
| [프로그래머스] 숫자짝꿍 (0) | 2023.04.02 |
|---|---|
| [프로그래머스] 이진수 더하기 (0) | 2023.03.18 |
| [프로그래머스] 베스트 앨범 (0) | 2023.03.14 |
| [python] 파이썬 re 모듈 동작 방식 (1) | 2023.03.13 |
| 최대 공약수, 최소 공배수 (0) | 2023.03.03 |



